7. Trigonometric Substitutions
a3. Substitutions for \(x^2-1\) (or \(1-x^2\)) - Secant Substitutions
Recall the derivative and integral formulas for \(\mathrm{arcsec}\,x\): \[ \dfrac{d}{dx}\mathrm{arcsec}\,x=\dfrac{1}{|x|\sqrt{x^2-1}} \qquad \qquad \qquad \int \dfrac{1}{|x|\sqrt{x^2-1}}\,dx=\mathrm{arcsec}\,x+C \] and the second Pythagorean Trig Identity written as: \[ \sec^2\theta-1=\tan^2\theta \]
These formulas motivate the following integration technique:
If the integrand involves the quantity \(x^2-1\) (or \(1-x^2\)) and
you know that \(|x| \ge 1\), then it may be useful to make the
substitution \(x=\sec\theta\). Then \(dx=\sec\theta\tan\theta\,d\theta\)
and \(x^2-1=\sec^2\theta-1=\tan^2\theta\). So it may be possible to
re-express the integrand in terms of \(\sec\theta\) and \(\tan\theta\) only.
Why do you need to know \(|x| \ge 1\)?
Since \(|\sec\theta| \ge 1\), if \(|x| \lt 1\) then we cannot set \(x=\sec\theta\).
Graph of \(\sec\theta\).
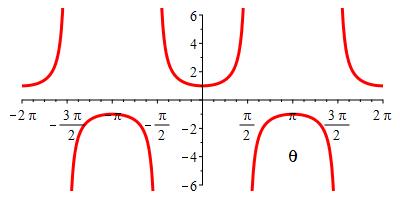
How do you know if \(|x| \ge 1\)?
You look at any quantities inside square roots such as \(\sqrt{x^2-1}\) or at the limits on the integral.
Here are some examples:
Compute \(\displaystyle \int \dfrac{(x^2-1)^{3/2}}{x}\,dx\).
Since \(x^2-1\) is raised to the \(\dfrac{3}{2}\) power, we must have \(x^2-1 \ge 0\). So \(x^2 \ge 1\) or \(|x| \ge 1\). So we substitute \(x=\sec\theta\). Then \(dx=\sec\theta\tan\theta\,d\theta\) and: \[\begin{aligned} \int \dfrac{(x^2-1)^{3/2}}{x}\,dx &=\int \dfrac{(\sec^2\theta-1)^{3/2}}{\sec\theta} \sec\theta\tan\theta\,d\theta \\ &=\int \dfrac{\tan^3\theta}{\sec\theta} \sec\theta\tan\theta\,d\theta =\int \tan^4\theta\,d\theta \end{aligned}\] We now use the identity \(\tan^2\theta=\sec^2\theta-1\) twice to write: \[\begin{aligned} \tan^4\theta &=\tan^2\theta(\sec^2\theta-1) =\tan^2\theta\sec^2\theta-\tan^2\theta \\ &=\tan^2\theta\sec^2\theta-\sec^2\theta+1 \end{aligned}\] So: \[\begin{aligned} \int \dfrac{(x^2-1)^{3/2}}{x}\,dx &=\int (\tan^2\theta\sec^2\theta-\sec^2\theta+1)\,d\theta \\ &=\dfrac{\tan^3\theta}{3}-\tan\theta+\theta+C \end{aligned}\] Don't forget to substitute for the differential! Don't forget to substitute back! We now substitute back. We already know that \(\sec\theta=x\) from the definition of the substitution. So: \[ \theta=\mathrm{arcsec}\,x \] We need a formula for \(\tan\theta\) in terms of \(x\). There are two ways to find this formula:
We can use the Pythagorean identity \(\tan^2\theta=\sec^2\theta-1\). So: \[ \tan\theta=\sqrt{\sec^2\theta-1}=\sqrt{x^2-1} \]
We can draw a right triangle with an angle \(\theta\) whose hypotenuse is \(x\) and whose adjacent side is \(1\). These sides are chosen so that \(\sec\theta=\dfrac{x}{1}=x\). Then the opposite side is \(\sqrt{x^2-1}\) and so: \[ \tan\theta=\sqrt{x^2-1} \]
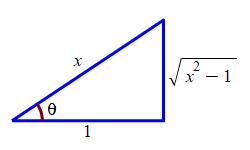
In either case the original integral is: \[\begin{aligned} \int \dfrac{(x^2-1)^{3/2}}{x}\,dx &=\dfrac{\tan^3\theta}{3}-\tan\theta+\theta+C \\ &=\dfrac{(x^2-1)^{3/2}}{3}-\sqrt{x^2-1}+\mathrm{arcsec}\,x+C \end{aligned}\]
We check by differentiating. If \(f=\dfrac{(x^2-1)^{3/2}}{3}-\sqrt{x^2-1}+\mathrm{arcsec}\,x\), then \[\begin{aligned} f'(x) &=x(x^2-1)^{1/2}-\dfrac{x}{\sqrt{x^2-1}}+\dfrac{1}{x\sqrt{x^2-1}} \\ &=\dfrac{x^2(x^2-1)-x^2+1}{x\sqrt{x^2-1}} =\dfrac{x^4-2x^2+1}{x\sqrt{x^2-1}} \\ &=\dfrac{(x^2-1)^2}{x\sqrt{x^2-1}} =\dfrac{(x^2-1)^{3/2}}{x} \end{aligned}\] which is the integrand we started with.
Compute \(\displaystyle \int_{\sqrt{2}}^2 \dfrac{1}{1-x^2}\,dx\).
From the limits, we see that \(\sqrt{2} \le x \le 2\) and hence \(|x| \gt 1\). So we substitute \(x=\sec\theta\). Then \(dx=\sec\theta\tan\theta\,d\theta\). Rather than substituting back, we change limits. So: \[\begin{aligned} \int_{\sqrt{2}}^2 &\dfrac{1}{1-x^2}\,dx =\int_{\pi/4}^{\pi/3} \dfrac{1}{1-\sec^2\theta}\sec\theta\tan\theta\,d\theta \\ &=\int_{\pi/4}^{\pi/3} \dfrac{1}{-\tan^2\theta}\sec\theta\tan\theta\,d\theta =-\int_{\pi/4}^{\pi/3} \dfrac{\sec\theta}{\tan\theta}\,d\theta \\ &=-\int_{\pi/4}^{\pi/3} \dfrac{1}{\sin\theta}\,d\theta =-\int_{\pi/4}^{\pi/3} \csc\theta\,d\theta \\ &=-\left[\dfrac{}{}-\ln|\csc\theta+\cot\theta|\right]_{\pi/4}^{\pi/3} \\ \end{aligned}\]
We check by differentiating. If \(f=-\ln|\csc\theta+\cot\theta|\), then \[\begin{aligned} f'(x) &=-\,\dfrac{-\csc\theta\cot\theta-\csc^2\theta}{\csc\theta+\cot\theta} \\ &=\dfrac{\csc\theta(\cot\theta+\csc\theta)}{\csc\theta+\cot\theta} =\csc\theta \end{aligned}\] This is a formula to remember like the one for \(\displaystyle \int \sec\theta\,d\theta\).
Finally, we evaluate at the limits: \[\begin{aligned} \int_{\sqrt{2}}^2 \dfrac{1}{1-x^2}\,dx &=\ln\left|\csc\dfrac{\pi}{3}+\cot\dfrac{\pi}{3}\right| -\ln\left|\csc\dfrac{\pi}{4}+\cot\dfrac{\pi}{4}\right| \\ &=\ln\left|\dfrac{2}{\sqrt{3}}+\dfrac{1}{\sqrt{3}}\right| -\ln|\sqrt{2}+1| \\ &=\ln\sqrt{3}-\ln(\sqrt{2}+1) \end{aligned}\]
Now it's your turn:
Compute \(\displaystyle \int \dfrac{\sqrt{x^2-1}}{x}\,dx\).
Let \(x=\sec\theta\).
\(\displaystyle \int \dfrac{\sqrt{x^2-1}}{x}\,dx =\sqrt{x^2-1}-\mathrm{arcsec}\,x+C\)
We substitute \(x=\sec\theta\). Then \(dx=\sec\theta\tan\theta\,d\theta\) and: \[\begin{aligned} \int \dfrac{\sqrt{x^2-1}}{x}\,dx &=\int \dfrac{\sqrt{\sec^2\theta-1}}{\sec\theta}\sec\theta\tan\theta\,d\theta =\int \tan^2\theta\,d\theta \\ &=\int (\sec^2\theta-1)\,d\theta =\tan\theta-\theta +C\\ \end{aligned}\] To substitute back, we have \(\sec\theta=x\) and so \(\theta=\mathrm{arcsec}\,x\). From either the Pythagorean identity or the triangle plot, we have: \[ \tan\theta=\sqrt{\sec^2\theta-1}=\sqrt{x^2-1} \] So: \[ \int \dfrac{\sqrt{x^2-1}}{x}\,dx =\sqrt{x^2-1}-\mathrm{arcsec}\,x+C \]
We check by differentiating. If \(f(x)=\sqrt{x^2-1}-\mathrm{arcsec}\,x\), then \[\begin{aligned} f'(x) &=\dfrac{1}{2}\dfrac{2x}{\sqrt{x^2-1}}-\dfrac{1}{x\sqrt{x^2-1}} \\ &=\dfrac{x^2-1}{x\sqrt{x^2-1}} \\ &=\dfrac{\sqrt{x^2-1}}{x} \end{aligned}\] which is the integrand we started with.
Compute \(\displaystyle \int \dfrac{x}{(1-x^2)^2}\,dx\) assuming \(|x|>1\).
Let \(x=\sec\theta\). Or use the ordinary substitution \(u=1-x^2\).
\(\displaystyle \int \dfrac{x}{(1-x^2)^2}\,dx =\dfrac{1}{2(1-x^2)}+C\)
We substitute \(x=\sec\theta\) and \(dx=\sec\theta\tan\theta\,d\theta\): \[\begin{aligned} \int \dfrac{x}{(1-x^2)^2}\,dx &=\int \dfrac{\sec\theta}{(1-\sec^2\theta)^2}\sec\theta\tan\theta\,d\theta \\ &=\int \dfrac{\sec^2\theta}{\tan^3\theta}\,d\theta \end{aligned}\] Now let \(u=\tan\theta\). Then \(du=\sec^2\theta\,d\theta\). So: \[ \int \dfrac{x}{(1-x^2)^2}\,dx =\int \dfrac{1}{u^3}\,du =\dfrac{1}{-2u^2}+C \] Finally we substitute back: \[\begin{aligned} \int \dfrac{x}{(1-x^2)^2}\,dx &=-\,\dfrac{1}{2\tan^2\theta}+C =-\,\dfrac{1}{2(\sec^2\theta-1)}+C \\ &=\dfrac{1}{2(1-x^2)}+C \end{aligned}\] This solution was unnecessarily complicated. Always look for an ordinary substitution first:
We substitute \(u=1-x^2\). Then \(du=-2x\,dx\) and \(-\,\dfrac{1}{2}\,du=x\,dx\). So, \[\begin{aligned} \int \dfrac{x}{(1-x^2)^2}\,dx &=-\,\dfrac{1}{2}\int \dfrac{1}{u^2}\,du =\dfrac{1}{2u}+C \\ &=\dfrac{1}{2(1-x^2)}+C \end{aligned}\]
We check by differentiating. If \(f(x)=\dfrac{1}{2(1-x^2)}\), then \[\begin{aligned} f'(x) &=-\,\dfrac{1}{2}\dfrac{-2x}{(1-x^2)^2} \\ &=\dfrac{x}{(1-x^2)^2} \end{aligned}\] which is the integrand we started with.
It is interesting that the integrand and the answer to this last exercise (which used a \(\sec\) substitution) are the same as that for the last exercise on the previous page (which used a \(\sin\) substitution). However, it is not surprising since they can both be done with the same ordinary substitution. On the other hand, if you just ask for the antiderivative of \(\dfrac{x}{(1-x^2)^2}\), then the answer is \(\dfrac{1}{2(1-x^2)}+C\), but the constant of integration \(C\) might be different in each of the three intervals \((-\infty,-1)\), \((-1,1)\) and\((1,\infty)\).
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum